安装 matplotlib 库和 d2l 库

1
2
3
conda activate d2l
pip install matplotlib
pip install d2l

验证安装

1
2
3
4
import matplotlib
print(matplotlib.__version__)
import d2l
print(d2l.__version__)

导数和微分

假设我们有一个函数$f: \mathbb{R} \rightarrow \mathbb{R}$，其输入和输出都是标量，如果$f$的导数存在，这个极限被定义为：
$$
f’(x) = \lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h}.
$$
如果$f’(a)$存在，则称$f$在$a$处是可微（differentiable）的。

1
2
3
4
5
6
7
%matplotlib inline    
import numpy as np
from matplotlib_inline import backend_inline
from d2l import torch as d2l

def f(x):
    return 3 * x ** 2 - 4 * x
  • %matplotlib inline：Jupyter Notebook 的 魔法命令，让 matplotlib 生成的图像直接嵌入在 Jupyter Notebook 的输出单元格中，而不是弹出一个单独的窗口
  • from matplotlib_inline import backend_inline：确保图像在 Jupyter Notebook 中 直接显示，而不会单独弹出窗口
  • from d2l import torch as d2l：从 d2l（《动手学深度学习》的官方库）中 导入 PyTorch 版本的工具包，d2l 封装了一些绘图、数据加载等功能，方便深度学习相关任务
1
2
3
4
5
6
7
def numerical_lim(f, x, h):
    return (f(x + h) - f(x)) / h

h = 0.1
for i in range(5):
    print(f'h={h:.5f}, numerical limit={numerical_lim(f, 1, h):.5f}')
    h *= 0.1
  • deff numerical_lim：定义导数
  • h={h:.5f}：格式化 h 为小数点后 5 位
  • numerical_lim(f, 1, h):.5f：计算 f(x) 在 x=1 处的导数，并格式化输出

等价符号

给定$y=f(x)$，其中$x$和$y$分别是函数$f$的自变量和因变量。以下表达式是等价的：
$$
f’(x) = y’ = \frac{dy}{dx} = \frac{df}{dx} = \frac{d}{dx} f(x) = Df(x) = D_x f(x)
$$

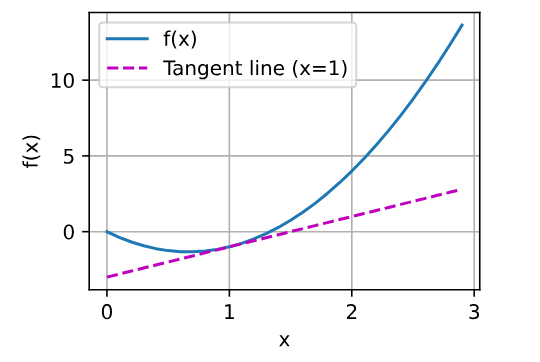
可视化

为了对导数的这种解释进行可视化，我们将使用matplotlib

use_svg_dieplay()

use_svg_display函数指定matplotlib软件包输出svg图表以获得更清晰的图像

1
2
3
def use_svg_display():  #@save
    """使用svg格式在Jupyter中显示绘图"""
    backend_inline.set_matplotlib_formats('svg')
  • backend_inline ： matplotlib_inline 库中的模块，用于控制 Jupyter Notebook 内嵌 Matplotlib 图像的显示格式
  • set_matplotlib_formats('svg') ：设置 Matplotlib 生成的图像格式为 SVG（可缩放矢量图）：
    • SVG（Scalable Vector Graphics） 是一种矢量图格式，放大后不会模糊，适合高分辨率显示（比如 Retina 屏幕）
    • 默认 Matplotlib 使用 PNG 格式，但 PNG 是像素图，放大会变模糊，而 SVG 保持清晰
  • #@save：d2l 库（《动手学深度学习》）的特殊标记：在 d2l 代码工具中自动保存这个函数，以便在后续 Notebook 运行时可以直接调用，而不需要重新定义

set_figsize()

定义set_figsize函数设置图表大小。

注意，这里可以直接使用d2l.plt，因为导入语句 from matplotlib import pyplot as plt已标记为保存到d2l包中

1
2
3
4
def set_figsize(figsize=(3.5, 2.5)):  #@save
    """设置matplotlib的图表大小"""
    use_svg_display()
    d2l.plt.rcParams['figure.figsize'] = figsize
  • def set_figsize(figsize=(3.5, 2.5))：定义一个函数 set_figsize()，默认图像大小为 (3.5, 2.5) 英寸（宽 3.5 英寸，高 2.5 英寸）
    • figsize 是一个 可选参数，允许用户自定义图像大小
  • use_svg_display()：确保 所有 Matplotlib 图像都以 SVG 格式显示
  • figure.figsize：控制 默认的 Matplotlib 图像尺寸，单位是 英寸（inch）
  • d2l.plt.rcParams['figure.figsize'] = figsize：修改 Matplotlib 所有后续图像的默认大小（用户 不需要每次手动设置 figsize，直接 plt.plot() 画图时就会应用这个默认尺寸）

set_axes()

set_axes函数用于设置自定义 Matplotlib 图表的坐标轴，包括：

  • 轴标签 (xlabel, ylabel)

  • 坐标轴范围 (xlim, ylim)

  • 坐标轴比例 (xscale, yscale)

  • 图例 (legend)

  • 网格 (grid())

1
2
3
4
5
6
7
8
9
10
11
12
#@save
def set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend):
    """设置matplotlib的轴"""
    axes.set_xlabel(xlabel)
    axes.set_ylabel(ylabel)
    axes.set_xscale(xscale)
    axes.set_yscale(yscale)
    axes.set_xlim(xlim)
    axes.set_ylim(ylim)
    if legend:
        axes.legend(legend)
    axes.grid()

  1. axes.set_xlabel(xlabel)&axes.set_ylabel(ylabel)

    分别 设置 x 轴和 y 轴的标签，用于描述数据含义

  2. axes.set_xscale(xscale)&axes.set_yscale(yscale)

    设置坐标轴的比例（scale）：

    • linear（线性比例，默认）
    • log（对数比例，适用于数据跨度较大的情况）

  3. axes.set_xlim(xlim)&axes.set_ylim(ylim)

    设置 x 轴和 y 轴的显示范围（xlim=(0, 10)表示 x 轴范围为[0, 10]）

  4. axes.legend(legend)：

    如果 legend 不为空，则添加图例（legend=["fro曲线1", "曲线2"]，就会在图中显示这些曲线名称）

  5. axes.grid()：显示网格

plot()

通过这三个用于图形配置的函数，定义一个plot函数来简洁地绘制多条曲线

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#@save
def plot(X, Y=None, xlabel=None, ylabel=None, legend=None, xlim=None,
         ylim=None, xscale='linear', yscale='linear',
         fmts=('-', 'm--', 'g-.', 'r:'), figsize=(3.5, 2.5), axes=None):
    """绘制数据点"""
    if legend is None:
        legend = []

    set_figsize(figsize)
    axes = axes if axes else d2l.plt.gca()

    # 如果X有一个轴，输出True
    def has_one_axis(X):
        return (hasattr(X, "ndim") and X.ndim == 1 or isinstance(X, list)                   and not hasattr(X[0], "__len__"))

    if has_one_axis(X):
        X = [X]
    if Y is None:
        X, Y = [[]] * len(X), X
    elif has_one_axis(Y):
        Y = [Y]
    if len(X) != len(Y):
        X = X * len(Y)
    axes.cla()
    for x, y, fmt in zip(X, Y, fmts):
        if len(x):
            axes.plot(x, y, fmt)
        else:
            axes.plot(y, fmt)
    set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend)

代码参数

参数 作用
X 横坐标数据，可以是一维数组或多条曲线的 x 轴数据
Y 纵坐标数据，可以是一维数组或多条曲线的 y 轴数据
xlabel / ylabel x 轴 / y 轴的标签
legend 图例（legend），用于标注不同曲线
xlim / ylim x 轴 / y 轴的范围（比如 (0,10)）
xscale / yscale 坐标轴的比例（默认为 linear，可以改为 log）
fmts 曲线样式，默认支持 - (实线)，m-- (紫色虚线)，g-. (绿色点划线)，r: (红色点线)
figsize 绘图尺寸（默认 (3.5, 2.5)）
axes 指定 Matplotlib 轴对象，如果为 None，则使用当前轴

设置图像大小

set_figsize()：

获取 Matplotlib 轴对象

axes = axes if axes else d2l.plt.gca()：如果 axes 参数 为空，则调用 d2l.plt.gca() 获取当前轴对象（Matplotlib 的 gca() 返回当前的 axes）

检查 X 是否为一维数组

def has_one_axis(X)：检查 X 是否为一维数组

  • hasattr(X, "ndim") and X.ndim == 1：检查 X 是否是 NumPy 数组，并且是一维的
  • isinstance(X, list) and not hasattr(X[0], "__len__")：检查 X 是否是 Python 列表，并且列表中的 元素不是列表（即 X 是一维列表）

代码拆解：

  1. hasattr(X, "ndim")：hasattr 是一个 Python 内置函数，用于检查对象是否有某个属性。这里检查的是 X 是否有 ndim 属性（通常是 numpy 数组才会有 ndim 属性，它表示数组的维度）。
  2. X.ndim == 1：这检查 X 是否是一维数组。X.ndim 表示数组的维度。
  3. isinstance(X, list)：这检查 X 是否是一个 Python list 类型（即普通列表）
  4. not hasattr(X[0], "__len__")：这检查 X 中的第一个元素（X[0]）是否没有 __len__ 属性。__len__ 属性通常用于表示对象的长度（例如列表）。如果 X[0] 不是列表或其他可迭代对象，就说明 X 是一个一维的普通列表，而不是嵌套列表

处理X和Y数据

1
2
3
4
5
6
7
8
if has_one_axis(X):
    X = [X]  # 转换为列表的列表
if Y is None:
    X, Y = [[]] * len(X), X  # 交换 X 和 Y（如果只给了 Y）
elif has_one_axis(Y):
    Y = [Y]  # 转换为列表的列表
if len(X) != len(Y):
    X = X * len(Y)  # 复制 X，使 X 和 Y 的长度一致

  • 如果 X 是 一维数据，转换为 二维列表（X = [X]），这样可以绘制多条曲线

  • 如果 没有提供 Y，则 X 变为空列表，Y = X（支持 plot(Y) 的情况）

    实际意义：如果 Y 为空，则假定 X 实际上是 Y，并自动生成 X，Matplotlib 会自动使用索引 [0,1,2,...] 作为 X

  • 如果 Y 是 一维数据，转换为 二维列表（Y = [Y]）

  • 如果 X 和 Y 长度不匹配，复制 X 以匹配 Y 的长度（适用于 X 只有一组数据，而 Y 有多组）

example：

1
2
3
X = [1, 2, 3]
has_one_axis(X)  # True
X = [X]  # 变为 [[1, 2, 3]]
1
2
3
4
5
6
7
8
X = [1, 2, 3]
Y = None

# 变为：
X, Y = [[]] * len(X), X

print(X)  # [[], [], []]
print(Y)  # [1, 2, 3]
1
2
3
Y = [2, 4, 6]
has_one_axis(Y)  # True
Y = [Y]  # 变为 [[2, 4, 6]]
1
2
3
4
5
6
X = [[1, 2, 3]]  # 只有一个 X
Y = [[2, 4, 6], [3, 6, 9]]  # 两条曲线

X = X * len(Y)  # 复制 X
print(X)  
# [[1, 2, 3], [1, 2, 3]]

绘制曲线

1
2
3
4
5
6
axes.cla()  # 清除当前轴的内容
for x, y, fmt in zip(X, Y, fmts):
    if len(x):
        axes.plot(x, y, fmt)  # 绘制 (x, y)
    else:
        axes.plot(y, fmt)  # 仅绘制 y（x 省略时，Matplotlib 默认使用索引作为 x 轴）

  • axes.cla() 清除当前坐标轴的内容，避免重复绘制。

  • zip(X, Y, fmts)

    逐一取出x, y, fmt：

    • axes.plot(x, y, fmt) 画曲线（fmt 指定曲线样式）。
    • 如果 x 为空，则直接绘制 y，Matplotlib 默认 x = range(len(y))。

设置坐标轴

  • set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend)：统一设置坐标轴参数（坐标范围、刻度、比例、标签等）

例子

1
2
x = np.arange(0, 3, 0.1)
plot(x, [f(x), 2 * x - 3], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])

example

偏导数

将微分的思想推广到多元函数（multivariate function）上

设$y = f(x_1, x_2, \ldots, x_n)$是一个具有$n$个变量的函数，$y$关于第$i$个参数$x_i$的偏导数（partial derivative）为：
$$
\frac{\partial y}{\partial x_i} = \lim_{h \rightarrow 0} \frac{f(x_1, \ldots, x_{i-1}, x_i+h, x_{i+1}, \ldots, x_n) - f(x_1, \ldots, x_i, \ldots, x_n)}{h}.
$$

等价符号

对于偏导数的表示，以下是等价的：
$$
\frac{\partial y}{\partial x_i} = \frac{\partial f}{\partial x_i} = f_{x_i} = f_i = D_i f = D_{x_i} f.
$$

梯度

连结一个多元函数对其所有变量的偏导数，以得到该函数的梯度（gradient）向量

设函数$f:\mathbb{R}^n\rightarrow\mathbb{R}$的输入是一个$n$维向量$\mathbf{x}=[x_1,x_2,\ldots,x_n]^\top$，并且输出是一个标量，函数$f(\mathbf{x})$相对于$\mathbf{x}$的梯度是一个包含$n$个偏导数的向量:
$$
\nabla_{\mathbf{x}} f(\mathbf{x}) = \bigg[\frac{\partial f(\mathbf{x})}{\partial x_1}, \frac{\partial f(\mathbf{x})}{\partial x_2}, \ldots, \frac{\partial f(\mathbf{x})}{\partial x_n}\bigg]^\top
$$
其中$\nabla_{\mathbf{x}} f(\mathbf{x})$通常在没有歧义时被$\nabla f(\mathbf{x})$取代

常用结论

假设$\mathbf{x}$为$n$维向量，在微分多元函数时经常使用以下规则:

  • 对于所有$\mathbf{A} \in \mathbb{R}^{m \times n}$，都有$\nabla_{\mathbf{x}} \mathbf{A} \mathbf{x} = \mathbf{A}^\top$
  • 对于所有$\mathbf{A} \in \mathbb{R}^{n \times m}$，都有$\nabla_{\mathbf{x}} \mathbf{x}^\top \mathbf{A} = \mathbf{A}$
  • 对于所有$\mathbf{A} \in \mathbb{R}^{n \times n}$，都有$\nabla_{\mathbf{x}} \mathbf{x}^\top \mathbf{A} \mathbf{x} = (\mathbf{A} + \mathbf{A}^\top)\mathbf{x}$
  • $\nabla_{\mathbf{x}} |\mathbf{x} |^2 = \nabla_{\mathbf{x}} \mathbf{x}^\top \mathbf{x} = 2\mathbf{x}$

同样，对于任何矩阵$\mathbf{X}$，都有$\nabla_{\mathbf{X}} |\mathbf{X} |_F^2 = 2\mathbf{X}$

矩阵求导

链式法则

在深度学习中，多元函数通常是复合（composite）的， 所以难以应用上述任何规则来微分这些函数。幸运的是，链式法则可以被用来微分复合函数。

单变量函数

让我们先考虑单变量函数。假设函数$y=f(u)$和$u=g(x)$都是可微的，根据链式法则：
$$
\frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx}.
$$

任意数量的变量

假设可微分函数$y$有变量$u_1, u_2, \ldots, u_m$，其中每个可微分函数$u_i$都有变量$x_1, x_2, \ldots, x_n$。注意，$y$是$x_1, x_2， \ldots, x_n$的函数。对于任意$i = 1, 2, \ldots, n$，链式法则给出：
$$
\frac{\partial y}{\partial x_i} = \frac{\partial y}{\partial u_1} \frac{\partial u_1}{\partial x_i} + \frac{\partial y}{\partial u_2} \frac{\partial u_2}{\partial x_i} + \cdots + \frac{\partial y}{\partial u_m} \frac{\partial u_m}{\partial x_i}
$$

自动微分

例子

对函数$y=2\mathbf{x}^{\top}\mathbf{x}$关于列向量$\mathbf{x}$求导

1
2
3
4
5
6
7
8
9
10
11
12
13
import torch

x = torch.arange(4.0) # tensor([0., 1., 2., 3.])

x.requires_grad_(True)  # 等价于x=torch.arange(4.0,requires_grad=True)
x.grad  # 默认值是None

y = 2 * torch.dot(x, x) # tensor(28., grad_fn=<MulBackward0>)

y.backward()
x.grad # tensor([ 0.,  4.,  8., 12.])

x.grad == 4 * x # 验证：tensor([True, True, True, True])

  • requires_grad_(True)： 使 x 具有 自动求导 功能（梯度计算）

  • x.grad ：默认是 None，因为梯度只有在 backward() 调用后才会被计算

  • y.backward()：y 对 x 进行反向传播，计算梯度 dy/dx

  • grad_fn=<MulBackward0>：

    • grad_fn（Gradient Function）是 PyTorch 自动求导机制 (autograd) 记录的 计算历史，它指向了 生成这个张量的运算，从而支持反向传播
    • MulBackward0 代表乘法的反向传播（Backward 代表反向传播）

x的另一个函数

1
2
3
4
5
6
# 在默认情况下，PyTorch会累积梯度，我们需要清除之前的值
x.grad.zero_()
y = x.sum()
y.backward()
x.grad
# tensor([1., 1., 1., 1.])

非标量变量的反向传播

1
2
3
4
5
6
7
# 对非标量调用backward需要传入一个gradient参数，该参数指定微分函数关于self的梯度。
# 本例只想求偏导数的和，所以传递一个1的梯度是合适的
x.grad.zero_()
y = x * x
# 等价于y.backward(torch.ones(len(x)))
y.sum().backward()
x.grad # tensor([0., 2., 4., 6.])
  • x.grad.zero_()：清空 x.grad。在 PyTorch 中，backward() 不会自动清空 x.grad，如果不手动清除，梯度会 累积

注意：

在 PyTorch 中，backward() 的默认行为是 计算 y 对 x 的梯度，并存入 x.grad。但 backward() 只能对 标量（单个数值）调用，如果 y 是 张量（向量/矩阵），就必须手动指定如何计算梯度。

y类型 直接.backward() 需要y.sum()吗 解决方案
标量：shape=() ✔允许 ✗不需要 y.backward()
向量：shape=(n,) ✗报错 ✔需要 y.sum()或y.backward(torch.ones_like(y))
矩阵：shape=(m,n) ✗报错 ✔需要 y.sum()或y.backward(torch.ones_like(y))

分离计算

有时，我们希望将某些计算移动到记录的计算图之外。

例如，假设y是作为x的函数计算的，而z则是作为y和x的函数计算的。我们想计算z关于x的梯度，但由于某种原因，希望将y视为一个常数，并且只考虑到x在y被计算后发挥的作用。

这里可以分离y来返回一个新变量u，该变量与y具有相同的值，但丢弃计算图中如何计算y的任何信息。换句话说，梯度不会向后流经u到x。因此，下面的反向传播函数计算z=u*x关于x的偏导数，同时将u作为常数处理，而不是z=x*x*x关于x的偏导数。

1
2
3
4
5
6
7
x.grad.zero_()
y = x * x
u = y.detach()
z = u * x

z.sum().backward()
x.grad == u # tensor([True, True, True, True])
  • detach()：返回一个与 y 具有相同值的新张量 u，但不参与梯度计算。u 不会计算梯度，也不会影响 x.grad

随后在y上调用反向传播

1
2
3
x.grad.zero_()
y.sum().backward()
x.grad == 2 * x # tensor([True, True, True, True])

Python控制流的梯度计算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def f(a):
    b = a * 2
    while b.norm() < 1000:
        b = b * 2
    if b.sum() > 0:
        c = b
    else:
        c = 100 * b
    return c

a = torch.randn(size=(), requires_grad=True)
d = f(a)
d.backward()

a.grad == d / a # tensor(True)
  • torch.randn(size=()) 生成一个 零维（标量） 的随机数 a，其值服从 标准正态分布
  • requires_grad=True 使 a 参与自动求导

其他

为什么计算二阶导数比一阶导数的开销要更大？

  1. 计算图更复杂
  2. 需要存储更多的中间变量
  3. 计算二阶导数需要两次反向传播

在运行反向传播函数之后，立即再次运行它，看看会发生什么？

如果在没有设置 retain_graph=True 的情况下，立即再次运行 backward()，PyTorch 会报错：

1
2
3
4
5
6
7
8
9
x = torch.tensor(2.0, requires_grad=True)
y = x ** 3

y.backward()
x.grad # tensor(12.)

y.backward()
x.grad 
# RuntimeError: Trying to backward through the graph a second time, but the buffers have already been freed. Specify retain_graph=True when calling backward the first time.

为什么会报错

当 backward() 运行时，PyTorch 默认会释放计算图，以节省内存。因此：

  1. 第一次调用 y.backward()：
    • PyTorch 计算 dy/dx 并存储在 x.grad 里。
    • 计算完成后，PyTorch 释放计算图，清除所有用于计算梯度的中间变量。
  2. 第二次调用 y.backward()：
    • 由于计算图已经释放，PyTorch 无法再次计算梯度，因此报错。

如何避免这个问题

如果你想在 同一个计算图上多次调用 backward()，需要在第一次 backward() 时 保留计算图：

1
2
y.backward(retain_graph=True)  # 允许计算图保留
y.backward()  # 第二次运行，不会报错

什么时候需要多次 backward()？

  • 计算二阶导数（如 Hessian 矩阵）
  • 多次计算梯度（如在强化学习中的策略梯度方法）

但一般情况下，只需要一次 backward() 即可，无需 retain_graph=True

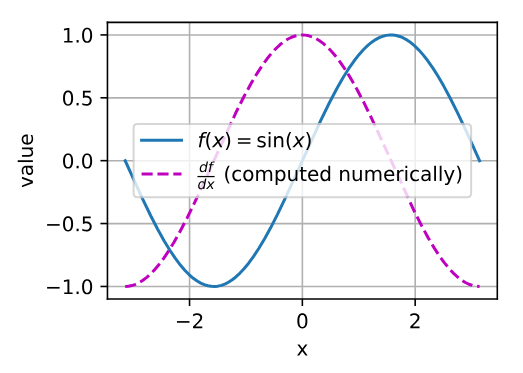
使$f(x)=\sin(x)$，绘制$f(x)$和$\frac{df(x)}{dx}$的图像，其中后者不使用$f’(x)=\cos(x)$

1
2
3
4
5
6
7
8
9
10
11
12
13
%matplotlib inline
from d2l import torch as d2l

x.grad.zero_()

x = torch.linspace(-1 * torch.pi, 1 * torch.pi, 1000, requires_grad=True)
y = torch.sin(x)

y.sum().backward()
dy_dx = x.grad

# 注意-绘图
d2l.plot(x.detach().numpy(), [y.detach().numpy(), dy_dx.detach().numpy()], 'x', 'value', legend=[r'$f(x) = \sin(x)$', r"$\frac{df}{dx}$ (computed numerically)"])

autograd_question

注意点

将 x、y 和 dy_dx 转换为 NumPy 数组 时，使用 .detach().numpy()：

1
d2l.plot(x.detach().numpy(), [y.detach().numpy(), dy_dx.detach().numpy()], 'x', 'value', legend=[r'$f(x) = \sin(x)$', r"$\frac{df}{dx}$ (computed numerically)"])

原因

在 PyTorch 中：

  • tensor.numpy() 不能用于 requires_grad=True 的张量
  • 需要先调用 tensor.detach()，这样 PyTorch 就不会追踪计算图，可以安全地转换为 NumPy

原理

**Pytorch 计算图与自动求导：**在 PyTorch 中，每当你对一个 requires_grad=True 的张量执行操作，PyTorch 会构建一张计算图，用于追踪所有计算，以便稍后进行 反向传播（backpropagation）。

**为什么 numpy() 不允许直接调用？：**当 requires_grad=True 时，直接调用 .numpy() 会破坏计算图，这会导致 PyTorch 无法继续反向传播。

如何解决？：detach() 方法的作用是 从计算图中分离张量，使其成为普通张量，不再追踪梯度。因此，我们可以先 detach() 再 numpy()