简单地说，机器学习就是做出预测

概率是一种灵活的语言，用于说明我们的确定程度，并且它可以有效地应用于广泛的领域中

基本概率论

掷骰子

%matplotlib inline
import torch
from torch.distributions import multinomial
from d2l import torch as d2l

fair_probs = torch.ones([6]) / 6
multinomial.Multinomial(1, fair_probs).sample() # tensor([0., 0., 0., 1., 0., 0.])

multinomial.Multinomial(10, fair_probs).sample() # tensor([1., 2., 2., 1., 1., 3.])

# 将结果存储为32位浮点数以进行除法
counts = multinomial.Multinomial(1000, fair_probs).sample()
counts / 1000  # 相对频率作为估计值
# tensor([0.1820, 0.1790, 0.1600, 0.1510, 0.1770, 0.1510])

创建公平骰子的概率分布

torch.distributions.multinomial：用于多项式分布采样（类似投掷骰子的实验）
fair_probs = torch.ones([6]) / 6：
- torch.ones([6]) 生成一个全为 1 的长度为 6 的张量（对应于 6 个骰子面）
- / 6 让每个面出现的概率都是 1/6，表示 公平骰子

torch.distributions.Multinomial(total_count, probs).sample(sample_shape=torch.Size([]))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

  - `total_count`：整数，表示 **一次实验中进行的独立试验次数**（比如投掷几次骰子）
  - `probs`：张量，表示 **每个类别（骰子面）的概率分布**（必须是非负数，且和为 1）
  - `sample_shape`（可选）：生成多个样本的形状，通常不需要指定

### 投掷10次骰子

- `Multinomial(10, fair_probs).sample()` **相当于投掷 10 次骰子**，统计每个面的出现次数

## 绘图

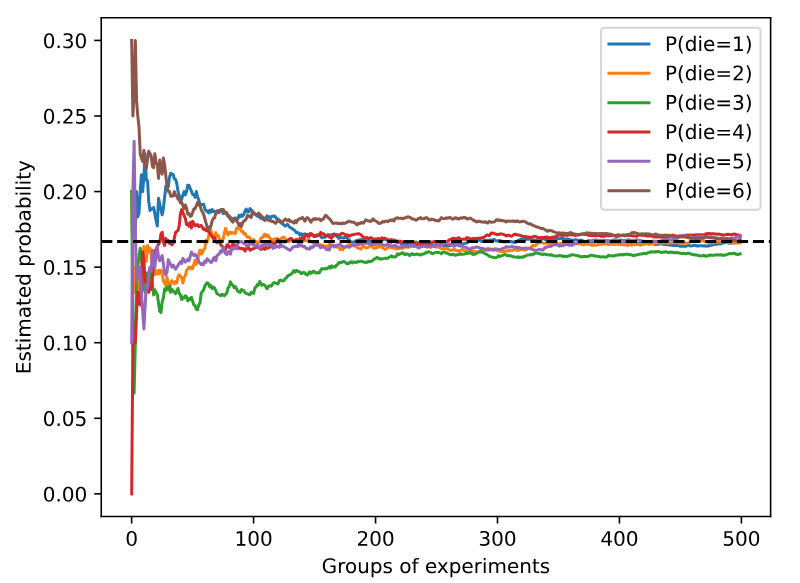
```python
counts = multinomial.Multinomial(10, fair_probs).sample((500,))
cum_counts = counts.cumsum(dim=0)
estimates = cum_counts / cum_counts.sum(dim=1, keepdims=True)

d2l.set_figsize((6, 4.5))
for i in range(6):
    d2l.plt.plot(estimates[:, i].numpy(),
                 label=("P(die=" + str(i + 1) + ")"))
d2l.plt.axhline(y=0.167, color='black', linestyle='dashed')
d2l.plt.gca().set_xlabel('Groups of experiments')
d2l.plt.gca().set_ylabel('Estimated probability')
d2l.plt.legend();

生成数据

multinomial.Multinomial(10, fair_probs).sample((500,))：
- 10：每次实验投掷 10 次骰子
- fair_probs：每个面出现的概率是 1/6
- sample((500,))：表示重复实验 500 组，结果 counts 是一个形状 (500, 6) 的张量，其中每一行表示 10 次投掷后各个面出现的次数。

计算累积出现次数

cum_counts = counts.cumsum(dim=0)：
- cumsum(dim=0) 按行累加，即 计算前 n 组实验的累计次数
- cum_counts[i] 表示前 i+1 组实验中各个骰子面出现的总次数

计算每个面的估计概率

estimates = cum_counts / cum_counts.sum(dim=1, keepdims=True)：
- cum_counts.sum(dim=1, keepdims=True) 计算每组实验的总投掷次数
- 每个面的累计出现次数 ÷ 总投掷次数 = 估计概率

画图

d2l.set_figsize((6, 4.5))：设置绘图大小，(6, 4.5) 表示宽 6、高 4.5

for i in range(6):
    d2l.plt.plot(estimates[:, i].numpy(),
                 label=("P(die=" + str(i + 1) + ")"))

estimates[:, i].numpy()：取出第 i 列的所有行数据，并转换为 NumPy 数组，以便 Matplotlib 可以绘制图像
- estimates 是一个 张量（Tensor），它的形状是 (500, 6)
- 索引 [:, i]：
  1. : 代表 取所有行（即 500 组实验）
  2. i 代表 取第 i 列（即骰子第 i+1 面的估计概率）
  3. 结果是一个 (500,) 形状的张量，表示 随着实验次数增加，骰子第 i+1 面的估计概率变化
- .numpy()：estimates[:, i] 是一个 PyTorch 张量（Tensor），但 Matplotlib 只能绘制 NumPy 数组，所以 .numpy() 将其转换为 NumPy 数组，方便绘制
- label=("P(die=" + str(i + 1) + ")")：添加图例，例如 P(die=1)、P(die=2) 等

添加参考线

d2l.plt.axhline(y=0.167, color='black', linestyle='dashed')：画一条 y=0.167 的 水平虚线（1/6 ≈ 0.167），表示理论概率

设置坐标轴和图例

set_xlabel('Groups of experiments')：x 轴表示 实验次数
set_ylabel('Estimated probability')：y 轴表示 每个面的估计概率
plt.legend()：显示图例（不同面的概率曲线）
d2l.plt.gca() 是 matplotlib.pyplot.gca() 的调用方式，它的作用是 获取当前的坐标轴（Axes）对象，用于进一步调整图表的格式
gca() 代表 “Get Current Axes”（获取当前坐标轴），它返回当前的 Axes 对象，允许我们对坐标轴进行更细致的调整，例如：
- 修改 x 轴和 y 轴的标签
- 调整刻度
- 设置标题
- 修改坐标轴的外观

概率论公理

概率（probability）可以被认为是将集合映射到真实值的函数。在给定的样本空间$\mathcal{S}$中，事件$\mathcal{A}$的概率，表示为$P(\mathcal{A})$，满足以下属性：

对于任意事件$\mathcal{A}$，其概率从不会是负数，即$P(\mathcal{A}) \geq 0$；
整个样本空间的概率为$1$，即$P(\mathcal{S}) = 1$；
对于互斥（mutually exclusive）事件（对于所有$i \neq j$都有$\mathcal{A}_i \cap \mathcal{A}_j = \emptyset$）的任意一个可数序列$\mathcal{A}_1, \mathcal{A}2, \ldots$，序列中任意一个事件发生的概率等于它们各自发生的概率之和，即 $P(\bigcup{i=1}^{\infty} \mathcal{A}i) = \sum{i=1}^{\infty} P(\mathcal{A}_i)$。

处理多个随机变量

联合概率

第一个被称为联合概率（joint probability）$P(A=a,B=b)$：$A=a$和$B=b$同时满足的概率

$P(A = a, B=b) \leq P(A=a)$

条件概率

$0 \leq \frac{P(A=a, B=b)}{P(A=a)} \leq 1$：我们称这个比率为条件概率（conditional probability）
$P(B=b \mid A=a)$

贝叶斯定理

$$
P(A \mid B) = \frac{P(B \mid A) P(A)}{P(B)}
$$

这里我们使用紧凑的表示法：其中$P(A, B)$是一个联合分布（joint distribution），$P(A \mid B)$是一个条件分布（conditional distribution）。这种分布可以在给定值$A = a, B=b$上进行求值。

边际化

$$
P(B) = \sum_{A} P(A, B)
$$

$B$的概率相当于计算$A$的所有可能选择，并将所有选择的联合概率聚合在一起：这也称为边际化（marginalization）。边际化结果的概率或分布称为边际概率（marginal probability）或边际分布（marginal distribution）。

独立性

$$
P(A, B) = P(A)P(B)
$$

如果两个随机变量$A$和$B$是独立的，意味着事件$A$的发生跟$B$事件的发生无关。在这种情况下，统计学家通常将这一点表述为$A \perp B$。

同样地，给定另一个随机变量$C$时，两个随机变量$A$和$B$是条件独立的（conditionally independent），当且仅当$P(A, B \mid C) = P(A \mid C)P(B \mid C)$。这个情况表示为$A \perp B \mid C$。

期望和方差

一个随机变量$X$的期望（expectation，或平均值（average））:
$$
E[X] = \sum_{x} x P(X = x)
$$
函数$f(x)$的输入是从分布$P$中抽取的随机变量：
$$
E_{x \sim P}[f(x)] = \sum_x f(x) P(x)
$$
衡量随机变量$X$与其期望值的偏差，可通过方差来量化：
$$
\mathrm{Var}[X] = E\left[(X - E[X])^2\right] =
E[X^2] - E[X]^2
$$
随机变量函数的方差衡量的是：当从该随机变量分布中采样不同值$x$时，函数值偏离该函数的期望的程度：
$$
\mathrm{Var}[f(x)] = E\left[\left(f(x) - E[f(x)]\right)^2\right]
$$
方差的平方根被称为标准差（standard deviation）