线性回归(深度学习)
回归(regression)是能为一个或多个自变量与因变量之间关系建模的一类方法
线性回归(linear regression)
线性回归的基本元素
- 线性模型
- 损失函数
- 解析解
- 随机梯度下降
- 用模型进行预测
例子
根据房屋的面积(平方英尺)和房龄(年)来估算房屋价格(美元)。
- 训练数据集(training data set) 或训练集(training set):房屋的销售价格、面积和房龄
- 样本(sample)/数据点(data point)或数据样本(data instance):每行数据
- 标签(label)或目标(target):试图预测的目标(比如预测房屋价格)
- 特征(feature)或协变量(covariate):预测所依据的自变量(面积和房龄)
线性模型
$$
\mathrm{price} = w_{\mathrm{area}} \cdot \mathrm{area} + w_{\mathrm{age}} \cdot \mathrm{age} + b
$$
- 权重(weight):$w_{\mathrm{area}}$和$w_{\mathrm{age}}$
- 偏置(bias)、偏移量(offset)或截距(intercept):$b$
机器学习领域,我们通常使用的是高维数据集,建模时采用线性代数表示法:
$$
\hat{y} = w_1 x_1 + … + w_d x_d + b
$$
$$
\hat{y} = \mathbf{w}^\top \mathbf{x} + b
$$
向量$\mathbf{x}$对应于单个数据样本的特征。用符号表示的矩阵$\mathbf{X} \in \mathbb{R}^{n \times d}$可以很方便地引用我们整个数据集的$n$个样本:
$$
{\hat{\mathbf{y}}} = \mathbf{X} \mathbf{w} + b
$$
过程中的求和将使用广播机制
我们很难找到一个有$n$个样本的真实数据集,其中对于所有的$1 \leq i \leq n$,$y^{(i)}$完全等于$\mathbf{w}^\top \mathbf{x}^{(i)}+b$。无论我们使用什么手段来观察特征$\mathbf{X}$和标签$\mathbf{y}$,都可能会出现少量的观测误差。因此,即使确信特征与标签的潜在关系是线性的,我们也会加入一个噪声项来考虑观测误差带来的影响。
在开始寻找最好的模型参数(model parameters)$\mathbf{w}$和$b$之前,我们还需要两个东西:
(1)一种模型质量的度量方式;
(2)一种能够更新模型以提高模型预测质量的方法。
损失函数
损失函数(loss function)能够量化目标的实际值与预测值之间的差距
平方误差函数:
$$
l^{(i)}(\mathbf{w}, b) = \frac{1}{2} \left(\hat{y}^{(i)} - y^{(i)}\right)^2
$$
由于平方误差函数中的二次方项, 估计值$\hat{y}^{(i)}$和观测值$y^{(i)}$之间较大的差异将导致更大的损失。 为了度量模型在整个数据集上的质量,我们需计算在$n$训练集个样本上的损失均值(也等价于求和):
$$
L(\mathbf{w}, b) =\frac{1}{n}\sum_{i=1}^n l^{(i)}(\mathbf{w}, b) =\frac{1}{n} \sum_{i=1}^n \frac{1}{2}\left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right)^2
$$
我们希望寻找一组参数($\mathbf{w}^, b^$),这组参数能最小化在所有训练样本上的总损失:
$$
\mathbf{w}^, b^ = \operatorname*{argmin}_{\mathbf{w}, b}\ L(\mathbf{w}, b)
$$
解析解
线性回归的解可以用一个公式简单地表达出来, 这类解叫作解析解(analytical solution)。
解析解可以进行很好的数学分析,但解析解对问题的限制很严格,导致它无法广泛应用在深度学习里。
随机梯度下降
梯度下降(gradient descent): 这种方法几乎可以优化所有深度学习模型。 它通过不断地在损失函数递减的方向上更新参数来降低误差
梯度下降最简单的用法是计算损失函数(数据集中所有样本的损失均值) 关于模型参数的导数(在这里也可以称为梯度)。
但实际中的执行可能会非常慢:因为在每一次更新参数之前,我们必须遍历整个数据集。 因此,我们通常会在每次需要计算更新的时候随机抽取一小批样本, 这种变体叫做小批量随机梯度下降(minibatch stochastic gradient descent)。
在每次迭代中,我们首先随机抽样一个小批量$\mathcal{B}$,它是由固定数量的训练样本组成的。然后,我们计算小批量的平均损失关于模型参数的导数(也可以称为梯度)。最后,我们将梯度乘以一个预先确定的正数$\eta$,并从当前参数的值中减掉:
$$
(\mathbf{w},b) \leftarrow (\mathbf{w},b) - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_{(\mathbf{w},b)} l^{(i)}(\mathbf{w},b)
$$
即:
$$
\mathbf{w} \leftarrow \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_{\mathbf{w}} l^{(i)}(\mathbf{w}, b) = \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \mathbf{x}^{(i)} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right)
$$
$$
b \leftarrow b - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_b l^{(i)}(\mathbf{w}, b) = b - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right)
$$
- 批量大小(batch size):$|\mathcal{B}|$
- 学习率(learning rate):$\eta$
- 超参数(hyperparameter):批量大小和学习率(可以调整但不在训练过程中更新的参数)
用模型预测
通过房屋面积$x_1$和房龄$x_2$来估计一个(未包含在训练数据中的)新房屋价格
矢量化加速
在训练我们的模型时,我们经常希望能够同时处理整个小批量的样本。 为了实现这一点,需要(我们对计算进行矢量化, 从而利用线性代数库,而不是在Python中编写开销高昂的for循环)
1 | %matplotlib inline |
__init__:在 Python 类中,__init__是 构造函数,用于 初始化类的实例。当你创建一个类的对象时,__init__方法会自动运行,为对象赋初始值np.array(self.times):把self.times(一个 Python 列表)转换为 NumPy 数组,方便进行数值运算.cumsum():计算累计和,即前面的所有数相加.tolist():把 NumPy 数组转换回 Python 列表,以便在 Python 代码中更容易使用
1 | c = torch.zeros(n) |
torch.zeros(n): 创建长度为n的全零张量c。timer = Timer(): 创建Timer计时器,并自动启动timer.stop(): 停止计时并返回运行时间f'{timer.stop():.5f} sec': 格式化时间,保留 5 位小数f'...':f-string(格式化字符串),用于插入变量值{}:占位符,用于插入变量或表达式的计算结果:.5f:格式化输出,.:表示小数点;5:保留 5 位小数;f:表示 浮点数格式
timer.start(): 重新启动计时器
正态分布与平方损失
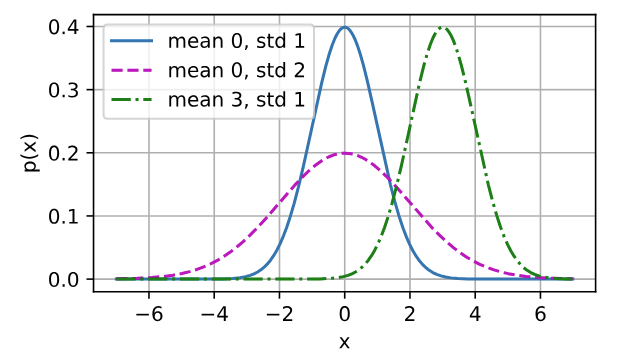
正态分布(normal distribution),也称为高斯分布(Gaussian distribution)
若随机变量$x$具有均值$\mu$和方差$\sigma^2$(标准差$\sigma$),其正态分布概率密度函数如下:
$$
p(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp\left(-\frac{1}{2 \sigma^2} (x - \mu)^2\right)
$$
1 | def normal(x, mu, sigma): |
均方误差损失函数(简称均方损失)可以用于线性回归的一个原因是: 我们假设了观测中包含噪声,其中噪声服从正态分布。 噪声正态分布如下式:
$$
y = \mathbf{w}^\top \mathbf{x} + b + \epsilon
$$
其中,$\epsilon \sim \mathcal{N}(0, \sigma^2)$
我们现在可以写出通过给定的$\mathbf{x}$观测到特定$y$的似然(likelihood):
$$
P(y \mid \mathbf{x}) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp\left(-\frac{1}{2 \sigma^2} (y - \mathbf{w}^\top \mathbf{x} - b)^2\right)
$$
根据极大似然估计法,参数$\mathbf{w}$和$b$的最优值是使整个数据集的似然最大的值:
$$
P(\mathbf y \mid \mathbf X) = \prod_{i=1}^{n} p(y^{(i)}|\mathbf{x}^{(i)})
$$
根据极大似然估计法选择的估计量称为极大似然估计量。虽然使许多指数函数的乘积最大化看起来很困难,但是我们可以在不改变目标的前提下,通过最大化似然对数来简化。由于历史原因,优化通常是说最小化而不是最大化。我们可以改为最小化负对数似然$-\log P(\mathbf y \mid \mathbf X)$。由此可以得到的数学公式是:
$$
-\log P(\mathbf y \mid \mathbf X) = \sum_{i=1}^n \frac{1}{2} \log(2 \pi \sigma^2) + \frac{1}{2 \sigma^2} \left(y^{(i)} - \mathbf{w}^\top \mathbf{x}^{(i)} - b\right)^2
$$
现在我们只需要假设$\sigma$是某个固定常数就可以忽略第一项,因为第一项不依赖于$\mathbf{w}$和$b$。现在第二项除了常数$\frac{1}{\sigma^2}$外,其余部分和前面介绍的均方误差是一样的。幸运的是,上面式子的解并不依赖于$\sigma$。因此,在高斯噪声的假设下,最小化均方误差等价于对线性模型的极大似然估计。