线性回归的从零开始实现（深度学习）

虽然现代的深度学习框架几乎可以自动化地进行所有这些工作，但从零开始实现可以确保我们真正知道自己在做什么。 同时，了解更细致的工作原理将方便我们自定义模型、自定义层或自定义损失函数

生成数据集

为了简单起见，我们将根据带有噪声的线性模型构造一个人造数据集。

任务

使用这个有限样本的数据集来恢复这个模型的参数

生成一个包含1000个样本的数据集，每个样本包含从标准正态分布中采样的2个特征。

使用线性模型参数$\mathbf{w} = [2, -3.4]^\top$、$b = 4.2$和噪声项$\epsilon$生成数据集及其标签：
$$
\mathbf{y}= \mathbf{X} \mathbf{w} + b + \mathbf\epsilon
$$
$\epsilon$可以视为模型预测和标签时的潜在观测误差。在这里我们认为标准假设成立，即$\epsilon$服从均值为0的正态分布。为了简化问题，我们将标准差设为0.01。

%matplotlib inline
import random
import torch
from d2l import torch as d2l

def synthetic_data(w, b, num_examples):  #@save
    """生成y=Xw+b+噪声"""
    X = torch.normal(0, 1, (num_examples, len(w)))
    y = torch.matmul(X, w) + b
    y += torch.normal(0, 0.01, y.shape)
    return X, y.reshape((-1, 1))

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)

print('features:', features[0],'\nlabel:', labels[0])
'''
features: tensor([0.6942, 2.7783]) 
label: tensor([-3.8680])
'''

d2l.set_figsize()
d2l.plt.scatter(features[:, 1].detach().numpy(), labels.detach().numpy(), 1);

• random：用于生成随机数
• X：形状为 (num_examples, len(w)) 的特征矩阵，每一行是一个样本。
• y：形状为 (num_examples, 1) 的标签列向量，符合 y = Xw + b + 噪声。
• torch.matmul 进行矩阵乘法（包括点积、矩阵-向量乘法和矩阵-矩阵乘法）
• y += torch.normal(0, 0.01, y.shape)：添加均值为 0，标准差为 0.01 的噪声
• reshape(-1, 1)：-1表示自动推导
• true_w = [2, -3.4]：设定真实权重
• true_b = 4.2：设定真实偏置项
• eatures, labels = synthetic_data(true_w, true_b, 1000)：
  • 生成 1000 个样本，每个样本有 2 个特征。
  • features 形状是 (1000, 2)，labels 形状是 (1000, 1)。
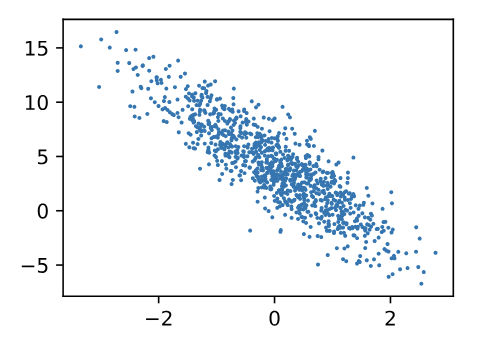
• d2l.set_figsize()：设置 Matplotlib 图像大小
• d2l.plt.scatter(features[:, 1].detach().numpy(), labels.detach().numpy(), 1);：
  • features[:, 1]：取所有样本的第二个特征（x2）。
  • labels：对应的标签值。
  • .detach().numpy()：将 PyTorch 张量转换为 NumPy 数组，方便 Matplotlib 处理。
  • plt.scatter(..., ..., 1)：绘制散点图，点大小设为 1。
• plt.scatter(x, y, s=None, c=None, marker=None, alpha=None, ...)：
  • x：散点图的 横坐标数据（可以是列表或 NumPy/PyTorch 张量）。
  • y：散点图的 纵坐标数据（可以是列表或 NumPy/PyTorch 张量）。
  • s：散点的大小（1 表示散点非常小）。
  • c：散点的颜色（可以是单个颜色或一个颜色数组）。
  • marker：散点的形状（如 'o'、's'、'x'）。
  • alpha：透明度（取值 0~1，1 表示不透明，0.5 表示半透明）。

读取数据集

训练模型时要对数据集进行遍历，每次抽取一小批量样本，并使用它们来更新我们的模型

由于这个过程是训练机器学习算法的基础，所以有必要定义一个函数， 该函数能打乱数据集中的样本并以小批量方式获取数据。

定义一个data_iter函数， 该函数接收批量大小、特征矩阵和标签向量作为输入，生成大小为batch_size的小批量。 每个小批量包含一组特征和标签。

def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    # 这些样本是随机读取的，没有特定的顺序
    random.shuffle(indices)
    for i in range(0, num_examples, batch_size):
        batch_indices = torch.tensor(
            indices[i: min(i + batch_size, num_examples)])
        yield features[batch_indices], labels[batch_indices]
        
batch_size = 10

for X, y in data_iter(batch_size, features, labels):
    print(X, '\n', y)
    break
    
'''
tensor([[-0.2324,  1.5688],
        [ 1.6030, -0.7080],
        [ 1.5979, -1.5452],
        [ 1.6035,  0.0764],
        [-0.6566,  1.9275],
        [-0.3860, -0.6425],
        [ 0.3464, -0.0370],
        [-0.9739,  1.1018],
        [ 1.1537, -0.4979],
        [-1.1189, -1.1404]]) 
 tensor([[-1.6054],
        [ 9.8046],
        [12.6415],
        [ 7.1550],
        [-3.6645],
        [ 5.5992],
        [ 4.9946],
        [-1.5033],
        [ 8.1968],
        [ 5.8229]])
'''

• num_examples = len(features)：获取数据集中样本的总数（1000 个）。

• indices = list(range(num_examples))：创建一个从 0 到 num_examples-1 的索引列表。

• andom.shuffle(indices)：随机打乱索引，确保每次抽取的数据是无序的（随机性）。

  （不会返回新的列表，而是就地修改原列表）

• for i in range(0, num_examples, batch_size)：

  • range(0, num_examples, batch_size)：从 0 开始，每次跳 batch_size 个样本。
  • 这样可以保证每次选取 batch_size 个数据点，直到遍历完整个数据集。

• batch_indices = torch.tensor(indices[i: min(i + batch_size, num_examples)])：

  • indices[i: min(i + batch_size, num_examples)]：
    • 取出当前批次的 batch_size 个索引。
    • min(i + batch_size, num_examples) 确保不会超出数据集范围。
  • torch.tensor(...)：将索引列表转换为 PyTorch 张量。

• yield features[batch_indices], labels[batch_indices]：

  • features[batch_indices]：按照随机索引，取出对应的特征值。
  • labels[batch_indices]：按照随机索引，取出对应的标签值。
  • yield 让函数成为 生成器，每次调用它时都会返回一个新的 batch 数据。

• 关键字	作用	运行后函数是否终止	适用于
  return	直接返回值	终止函数	普通函数
  yield	返回一个值，下次继续执行	不会终止，记住当前状态	生成器

• data_iter(batch_size, features, labels) 生成一个 批量数据的迭代器。

  for X, y in ... 获取每个小批量数据：

  • X 是当前 batch 的 特征张量，形状 (10, 2)（10 个样本，每个样本 2 个特征）。
  • y 是当前 batch 的 标签张量，形状 (10, 1)（10 个样本，每个样本 1 个标签）。

  break 只打印 第一个 batch，否则会继续遍历整个数据集。

初始化模型参数

在我们开始用小批量随机梯度下降优化我们的模型参数之前， 我们需要先有一些参数

w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

在初始化参数之后，我们的任务是更新这些参数，直到这些参数足够拟合我们的数据。

• torch.normal(0, 0.01, size=(2,1))

  • 生成一个2×1 的张量（即 2 行 1 列的矩阵）。

  • 数据服从均值 0，标准差 0.01 的正态分布（高斯分布）。

  • 这样做的目的是初始化 w 接近 0 的随机值，而不是全 0，防止梯度更新时陷入零梯度问题。

• requires_grad=True：让 PyTorch 记录 w 的梯度，用于后续反向传播计算 ∇w。

• torch.zeros(1, requires_grad=True)：

  • torch.zeros(1)：这部分代码创建了一个大小为 (1,) 的张量，其中唯一的元素是 0。这个张量表示模型的偏置 b，在初始化时设置为 0。

  • 1 表示张量的大小为 1（即只有一个元素）。

定义模型

接下来，我们必须定义模型，将模型的输入和参数同模型的输出关联起来。

要计算线性模型的输出，我们只需计算输入特征$\mathbf{X}$和模型权重$\mathbf{w}$的矩阵-向量乘法后加上偏置$b$。注意，上面的$\mathbf{Xw}$是一个向量，而$b$是一个标量。（广播机制）

def linreg(X, w, b):  #@save
    """线性回归模型"""
    return torch.matmul(X, w) + b

定义损失函数

这里我们使用平方损失函数。 在实现中，我们需要将真实值y的形状转换为和预测值y_hat的形状相同。

def squared_loss(y_hat, y):  #@save
    """均方损失"""
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

• y.reshape(y_hat.shape)：目的是将 y 的形状转换为和 y_hat 相同的形状。这是因为 y 和 y_hat 在训练时可能不是完全相同的形状，比如一个是列向量，一个是行向量。通过 reshape，我们确保两者的形状一致，便于进行差值计算。

定义优化算法

该函数接受模型参数集合、学习速率和批量大小作为输入。每 一步更新的大小由学习速率lr决定。

因为我们计算的损失是一个批量样本的总和，所以我们用批量大小（batch_size） 来规范化步长，这样步长大小就不会取决于我们对批量大小的选择。

def sgd(params, lr, batch_size):  #@save
    """小批量随机梯度下降"""
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()         

• sgd(params, lr, batch_size)：这是实现小批量随机梯度下降的函数。

  • params：包含所有模型参数（如权重和偏置）的列表。
  • lr：学习率（Learning Rate），它控制每次参数更新的步长。
  • batch_size：小批量的大小，表示一次训练中使用的样本数量。

• with torch.no_grad()：在更新参数时，禁用梯度计算。

  • 在 PyTorch 中，默认情况下，操作会记录梯度用于反向传播（反向传播会计算梯度）。而在更新参数时，我们不需要计算梯度，所以使用 torch.no_grad() 来确保更新过程不会干扰梯度计算，节省内存并加速计算。

• for param in params：对所有模型参数进行迭代（例如，权重和偏置）。

• param -= lr * param.grad / batch_size：这是参数更新的公式

  • param.grad：该参数的梯度，即损失函数相对于该参数的导数。这个值告诉我们该如何调整参数以减小损失。

  • lr：学习率，它决定了更新的步长。较高的学习率会导致参数大幅度调整，较低的学习率会使调整幅度较小。

  • / batch_size：因为我们采用的是小批量梯度下降，所以在计算梯度时是基于一个批次的样本，而不是整个数据集。为了使得每个样本对梯度的影响一致，需要除以 batch_size（批次大小），得到平均梯度。

  • param -= ...：更新规则：减去梯度的方向，因为我们要减少损失，梯度下降的方向是朝着损失减小的方向调整参数。

• param.grad.zero_()：每次参数更新之后，将参数的梯度清零。

  • 在 PyTorch 中，梯度是累加的。每次执行反向传播时，梯度会加到现有的梯度上。为了避免梯度累加影响下一次更新，我们需要在每次更新参数后清除梯度。zero_() 是一个原地操作，用于将 param.grad 清零。

训练

在每次迭代中，我们读取一小批量训练样本，并通过我们的模型来获得一组预测。 计算完损失后，我们开始反向传播，存储每个参数的梯度。 最后，我们调用优化算法sgd来更新模型参数。

概括一下，我们将执行以下循环：

• 初始化参数
• 重复以下训练，直到完成
  • 计算梯度$\mathbf{g} \leftarrow \partial_{(\mathbf{w},b)} \frac{1}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} l(\mathbf{x}^{(i)}, y^{(i)}, \mathbf{w}, b)$
  • 更新参数$(\mathbf{w}, b) \leftarrow (\mathbf{w}, b) - \eta \mathbf{g}$

在每个迭代周期（epoch）中，我们使用data_iter函数遍历整个数据集， 并将训练数据集中所有样本都使用一次（假设样本数能够被批量大小整除）。 这里的迭代周期个数num_epochs和学习率lr都是超参数，分别设为3和0.03。

lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y)  # X和y的小批量损失
        # 因为l形状是(batch_size,1)，而不是一个标量。l中的所有元素被加到一起，
        # 并以此计算关于[w,b]的梯度
        l.sum().backward()
        sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
        
'''
epoch 1, loss 0.041277
epoch 2, loss 0.000166
epoch 3, loss 0.000049
'''

print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')

'''
w的估计误差: tensor([ 0.0006, -0.0006], grad_fn=<SubBackward0>)
b的估计误差: tensor([0.0007], grad_fn=<RsubBackward1>)
'''

初始化参数

• lr 是学习率，控制每次参数更新的步长。

• num_epochs 是训练的轮数，表示数据集会被遍历多少次。

• net 是线性回归模型，假设是通过 linreg 函数定义的。这个模型会使用 w 和 b 作为参数。

• loss 是损失函数，选择的是均方误差（squared loss）。

训练过程

• for epoch in range(num_epochs)：循环遍历每一轮（epoch）。在每一轮中，所有训练数据都会被分批次处理。
• for X, y in data_iter(batch_size, features, labels)：这个循环遍历数据集的每个小批量（mini-batch）。X 和 y 分别是该批次的特征和标签。
• l = loss(net(X, w, b), y)：对于当前小批量数据，通过线性回归模型 net(X, w, b) 预测输出，并计算损失函数的值 l。其中，net(X, w, b) 计算的是预测结果，y 是真实标签。
• l.sum().backward()：计算损失函数关于 w 和 b 的梯度。l.sum() 是把所有批次样本的损失加和，以确保每次反向传播的梯度是整个批次的平均值。
• sgd([w, b], lr, batch_size)：使用小批量随机梯度下降（SGD）方法来更新参数 w 和 b。这个函数会根据学习率 lr 和批次大小 batch_size 来调整 w 和 b 的值。

评估损失

• with torch.no_grad()：在评估损失时，不需要计算梯度，因为我们只关心损失的值，而不需要更新参数。
• train_l = loss(net(features, w, b), labels)：计算整个数据集的损失（训练集的损失），以评估当前模型的性能。
• print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')：输出当前轮次的平均损失。

训练结果

• true_w 和 true_b 是线性回归模型的真实参数（生成数据时使用的参数）。

• w.reshape(true_w.shape)：确保 w 的形状与 true_w 一致。

• true_w - w.reshape(true_w.shape) 和 true_b - b：计算模型估计的参数与真实参数之间的误差，并输出。

脚本

%matplotlib inline
import random
import torch
from d2l import torch as d2l

def synthetic_data(w, b, num_examples):  #@save
    """生成y=Xw+b+噪声"""
    X = torch.normal(0, 1, (num_examples, len(w)))
    y = torch.matmul(X, w) + b
    y += torch.normal(0, 0.01, y.shape)
    return X, y.reshape((-1, 1))

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)

print('features:', features[0],'\nlabel:', labels[0])
'''
features: tensor([0.6942, 2.7783]) 
label: tensor([-3.8680])
'''

d2l.set_figsize()
d2l.plt.scatter(features[:, 1].detach().numpy(), labels.detach().numpy(), 1);

def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    # 这些样本是随机读取的，没有特定的顺序
    random.shuffle(indices)
    for i in range(0, num_examples, batch_size):
        batch_indices = torch.tensor(
            indices[i: min(i + batch_size, num_examples)])
        yield features[batch_indices], labels[batch_indices]
        
batch_size = 10

for X, y in data_iter(batch_size, features, labels):
    print(X, '\n', y)
    break
    
'''
tensor([[-0.2324,  1.5688],
        [ 1.6030, -0.7080],
        [ 1.5979, -1.5452],
        [ 1.6035,  0.0764],
        [-0.6566,  1.9275],
        [-0.3860, -0.6425],
        [ 0.3464, -0.0370],
        [-0.9739,  1.1018],
        [ 1.1537, -0.4979],
        [-1.1189, -1.1404]]) 
 tensor([[-1.6054],
        [ 9.8046],
        [12.6415],
        [ 7.1550],
        [-3.6645],
        [ 5.5992],
        [ 4.9946],
        [-1.5033],
        [ 8.1968],
        [ 5.8229]])
'''

w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

def linreg(X, w, b):  #@save
    """线性回归模型"""
    return torch.matmul(X, w) + b

def squared_loss(y_hat, y):  #@save
    """均方损失"""
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

def sgd(params, lr, batch_size):  #@save
    """小批量随机梯度下降"""
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()         
            
lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y)  # X和y的小批量损失
        # 因为l形状是(batch_size,1)，而不是一个标量。l中的所有元素被加到一起，
        # 并以此计算关于[w,b]的梯度
        l.sum().backward()
        sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
        
'''
epoch 1, loss 0.041277
epoch 2, loss 0.000166
epoch 3, loss 0.000049
'''

print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')

'''
w的估计误差: tensor([ 0.0006, -0.0006], grad_fn=<SubBackward0>)
b的估计误差: tensor([0.0007], grad_fn=<RsubBackward1>)
'''